Koch Polygons
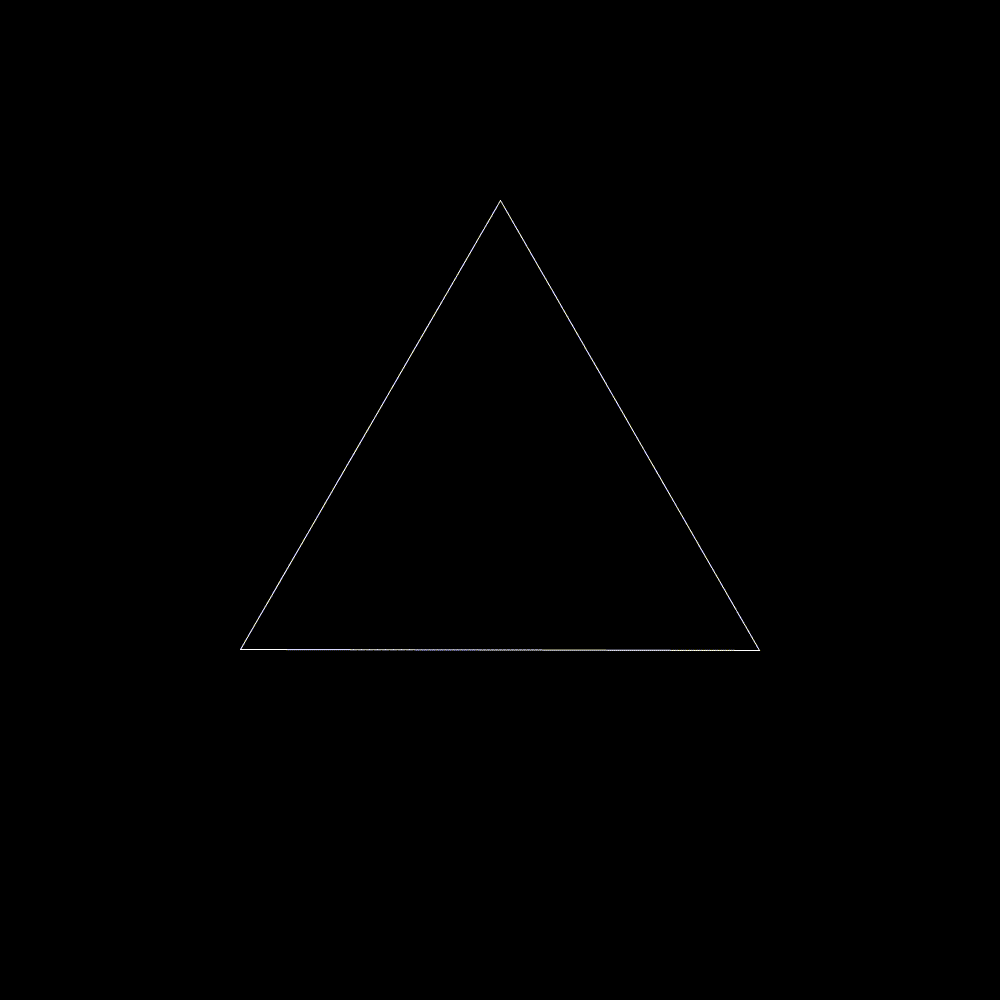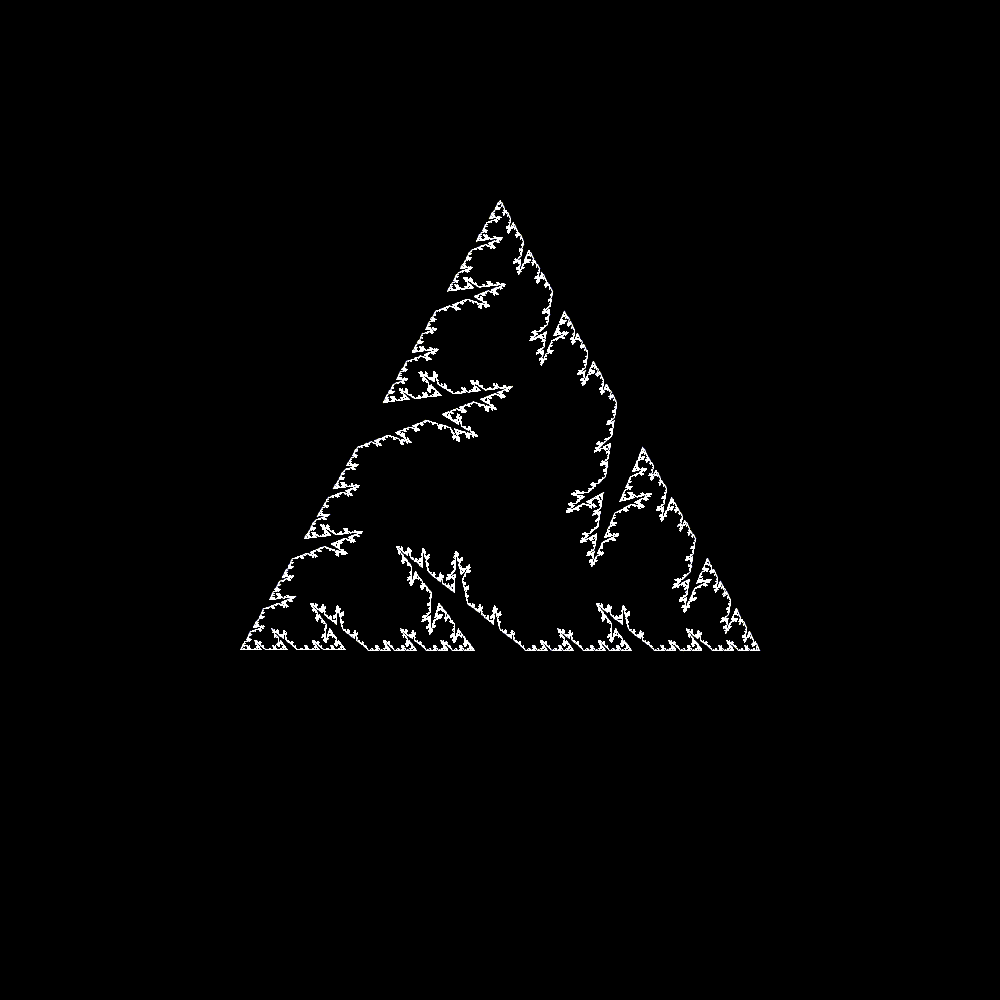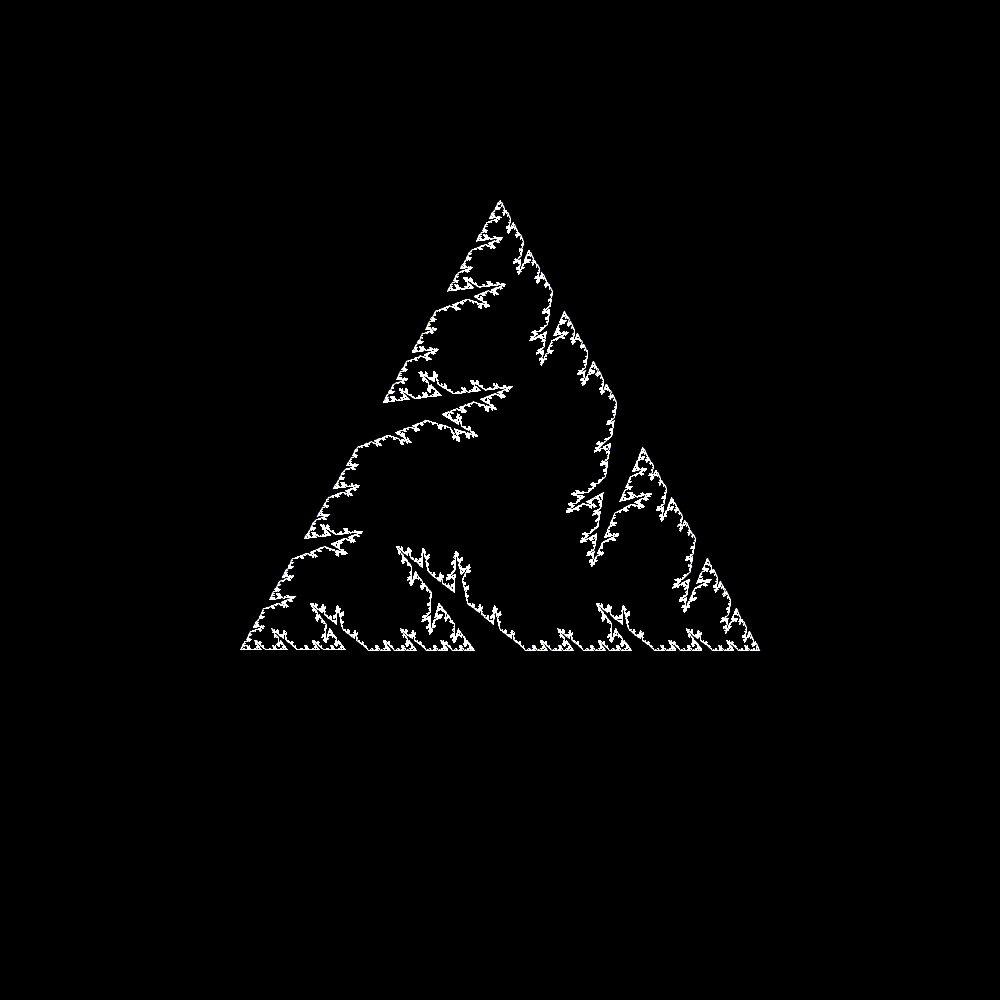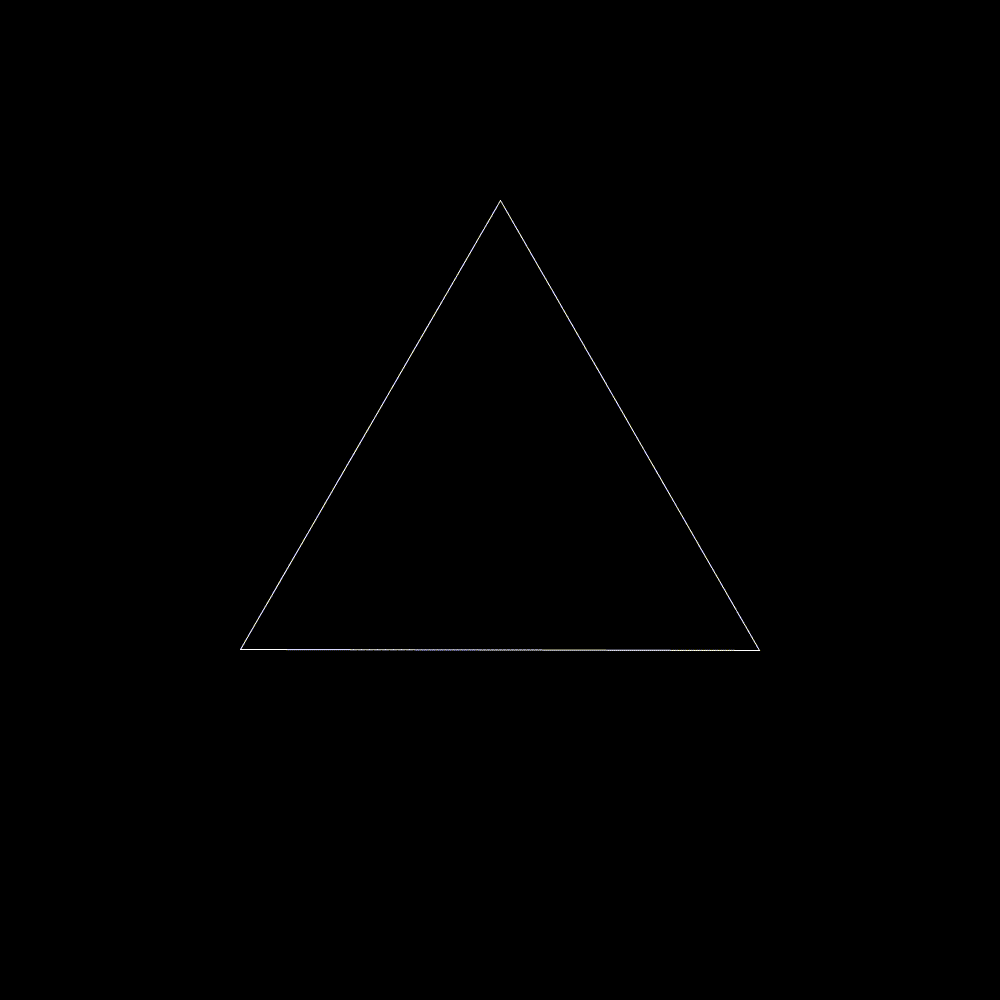
In 1904 a Swedish mathematician by the name of Helge von Koch published a paper concerning a continuous curve constructed from equilateral triangles. The curve is most well know in a form called the koch snowflake, one of the simplest and most recognizable fractals. The snowflake is build by repeatedly embedding equilateral triangles onto the sides of larger triangles. I’ve always been partial to the koch snowflake, as unlike many other fractals, even a non-mathematically inclined person can grasp and understand this simple recursive pattern.
The koch snowflake can be drawn very easily. Begin with an equilateral triangle, then for each side draw a smaller triangle with side lengths 1/3 the length of the embedding side. Thus we divide each side into 4 new segments, and create a star shaped dodecagon. A koch snowflake is the result of repeating this process infinitely, however because of the in-feasibility of computing such a figure the below demonstration repeats a mere 8 times.
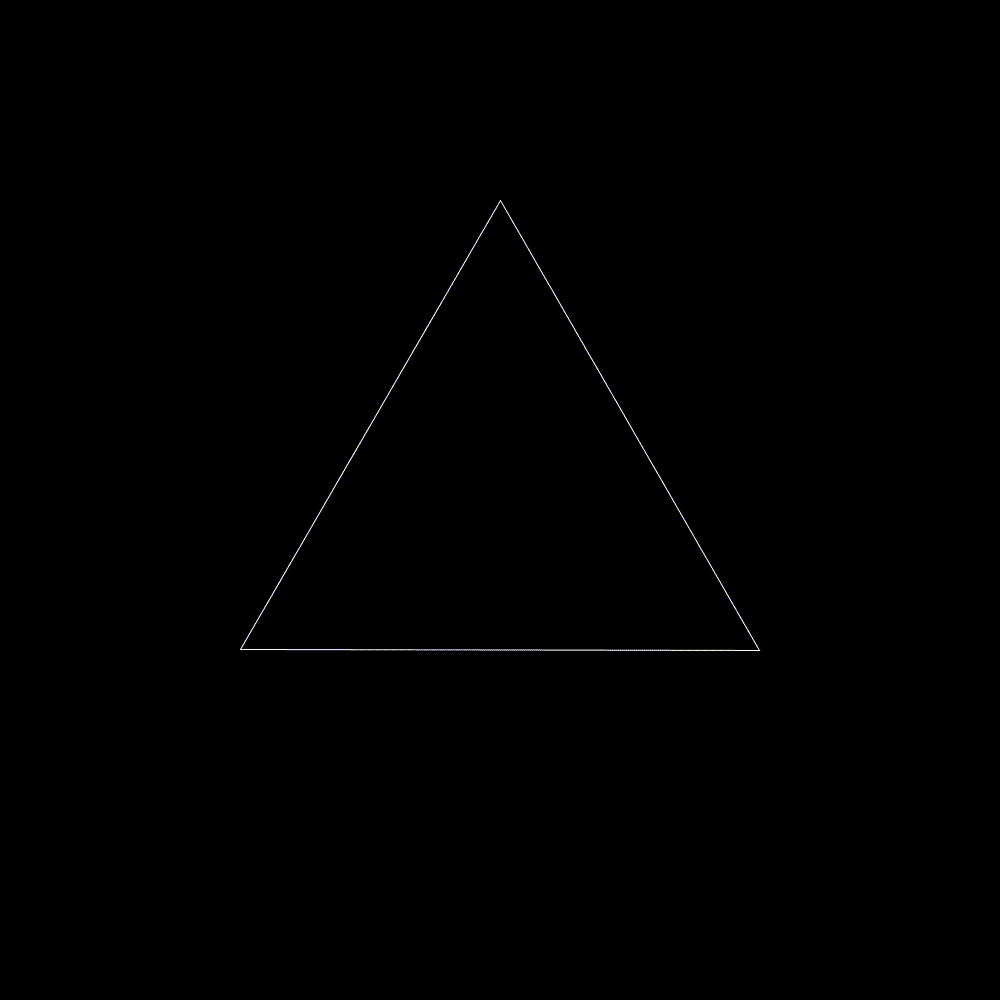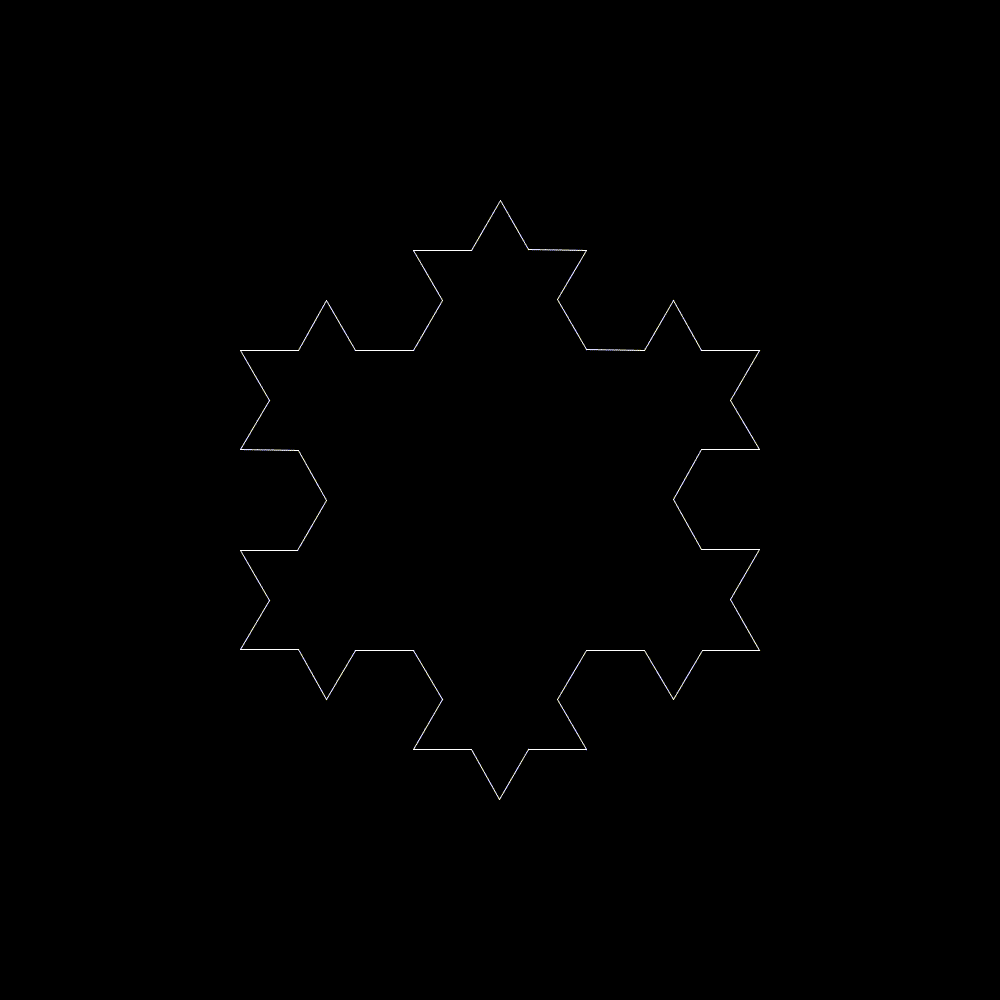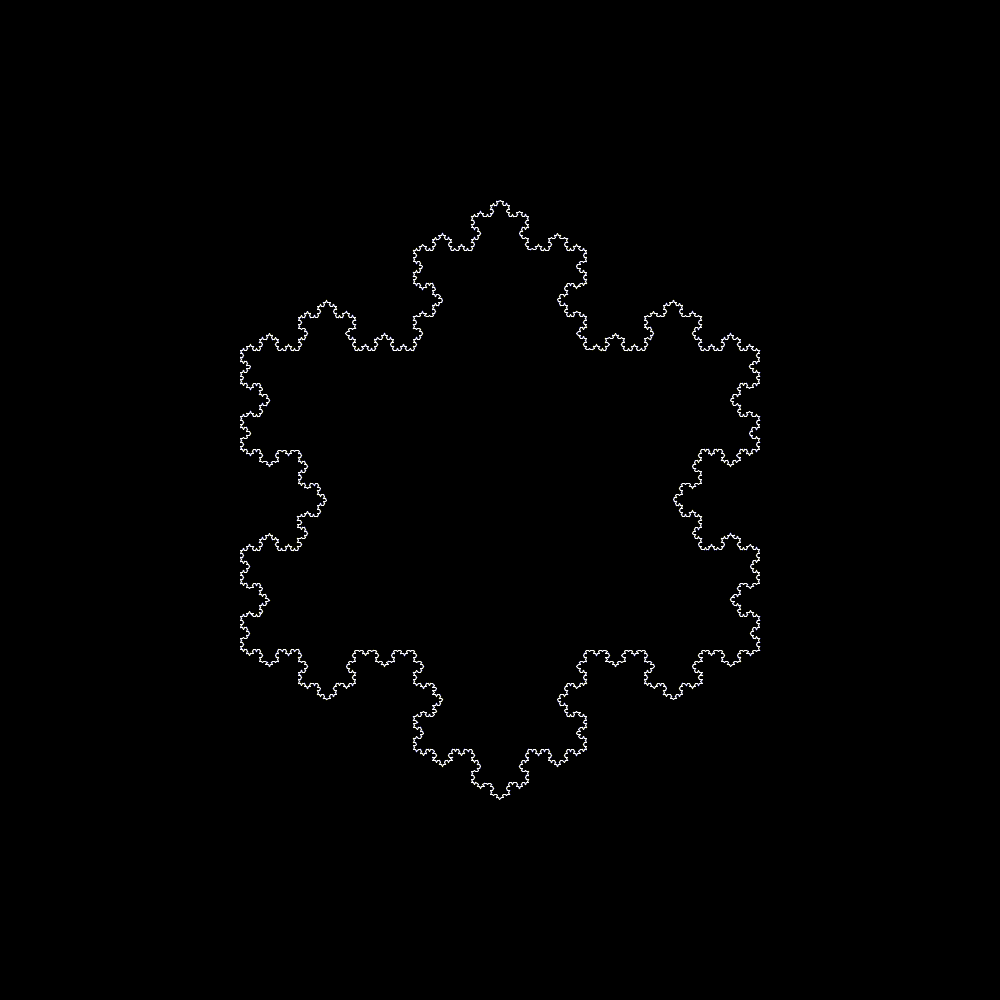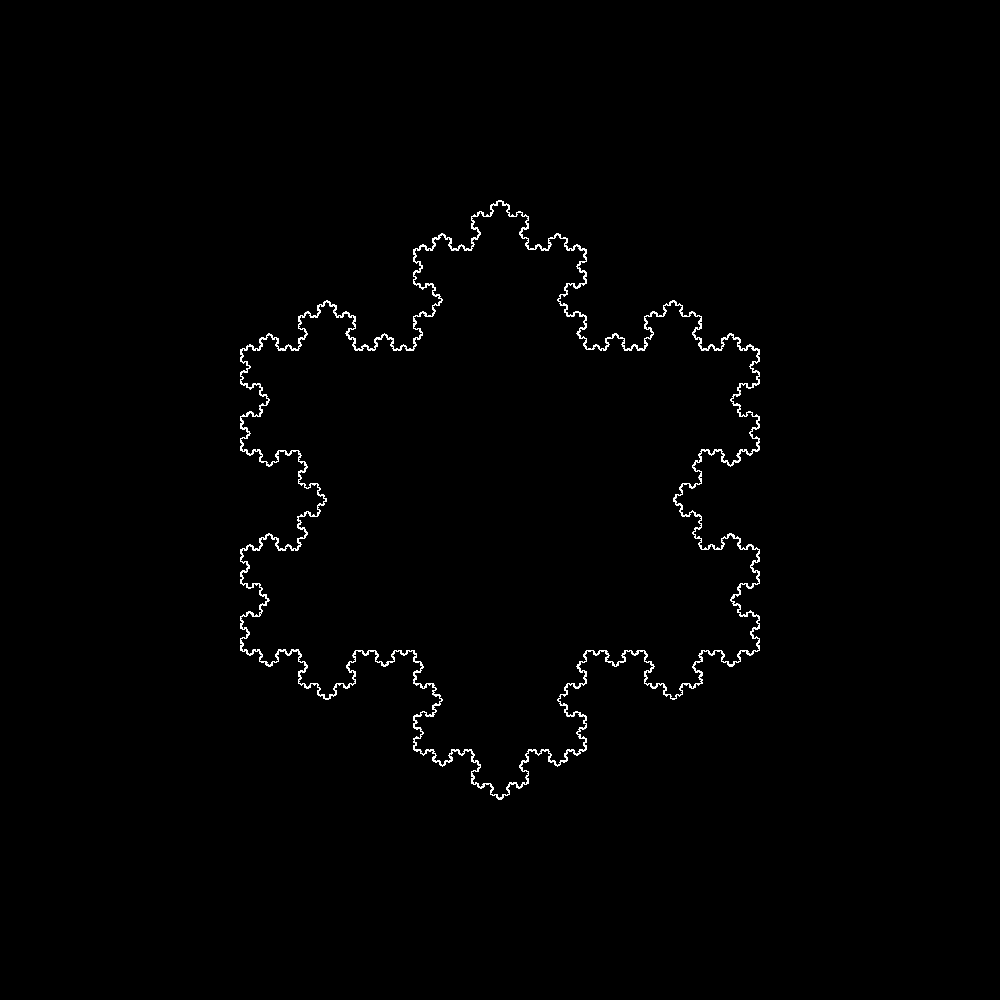
By generalizing this process over arbitrary side division schemes and starting polygons, more complex figures can be drawn. A small program I wrote in processing (which can be found here) does just this. It interprets a list of points within the unit square as a division pattern for a line. It then repeatedly applies this splitting pattern to a regular polygon drawing an approximation of the continuous curve defined by the split pattern.
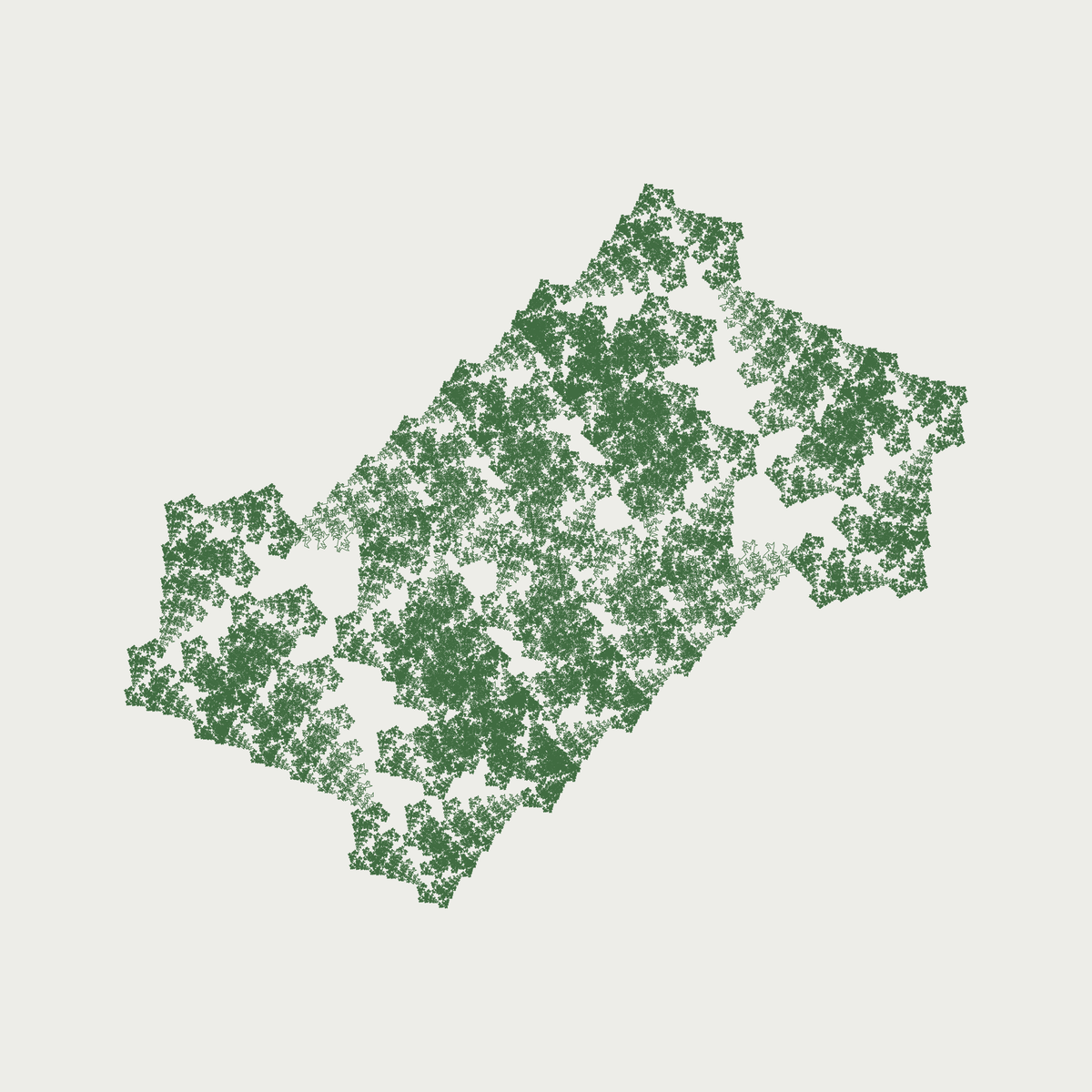
Here are some example koch polygons created with the program:



And five more rendered with a more colorful palette: